HiSET Math Study Guide: Measurement & Geometry
Measurement and geometry questions will assess your ability to:
- Describe and perform transformations in the plane
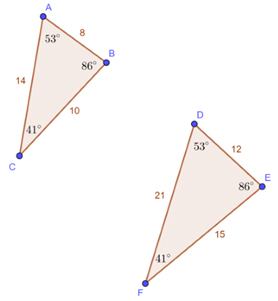
- Determine triangle similarity and congruence to solve problems
- Use properties of two-dimensional figures and angle relationships
- Solve for the volume and surface area of 3D figures
- Apply the Pythagorean theorem in various contexts
Transformations in the Plane
A transformation moves or changes a shape while maintaining its size or proportions. There are four main types:
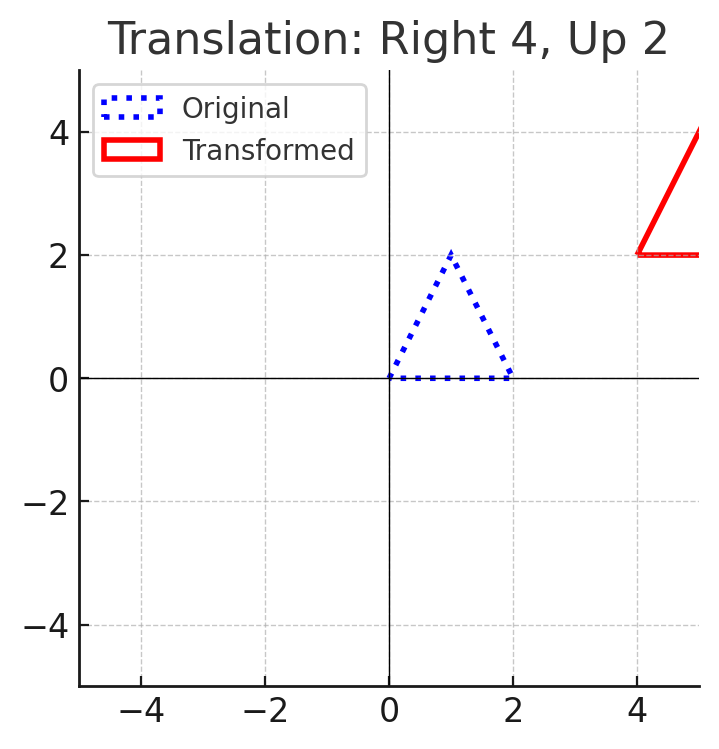
1. Translations (Slides)
- Moves a shape without rotating or flipping it.
- Every point shifts the same distance and direction.
- Example: Moving a triangle 4 units right and 2 units up.
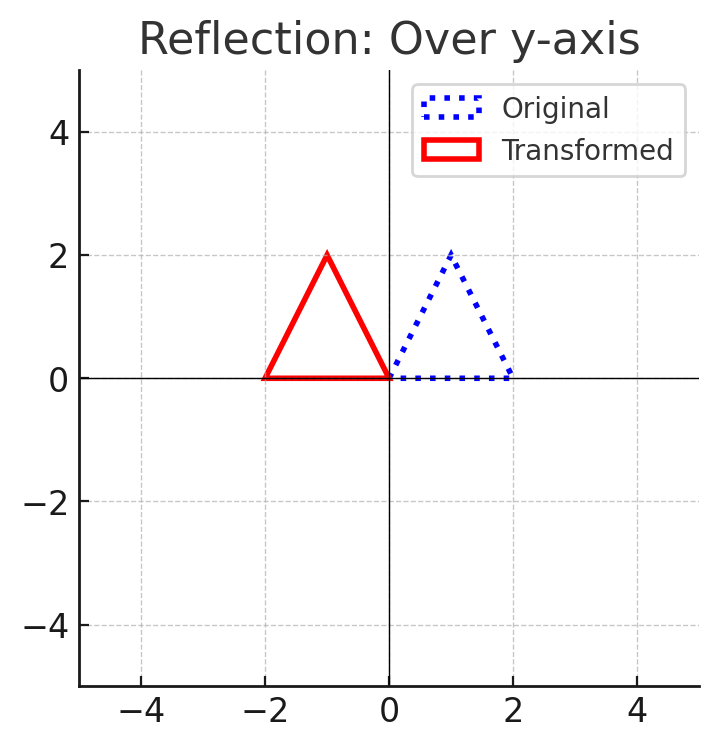
2. Reflections (Flips)
- Flips a shape over a line of reflection ($x$-axis, $y$-axis, or another line).
- The shape remains congruent but reversed.
- Example: Reflecting a triangle over the $y$-axis.
3. Rotations (Turns)
- Spins a shape around a fixed point, usually the origin $(0)$.
- Measured in degrees $(90°, 180°, 270°)$.
- Example: Rotating a triangle $90°$ counterclockwise around the origin.
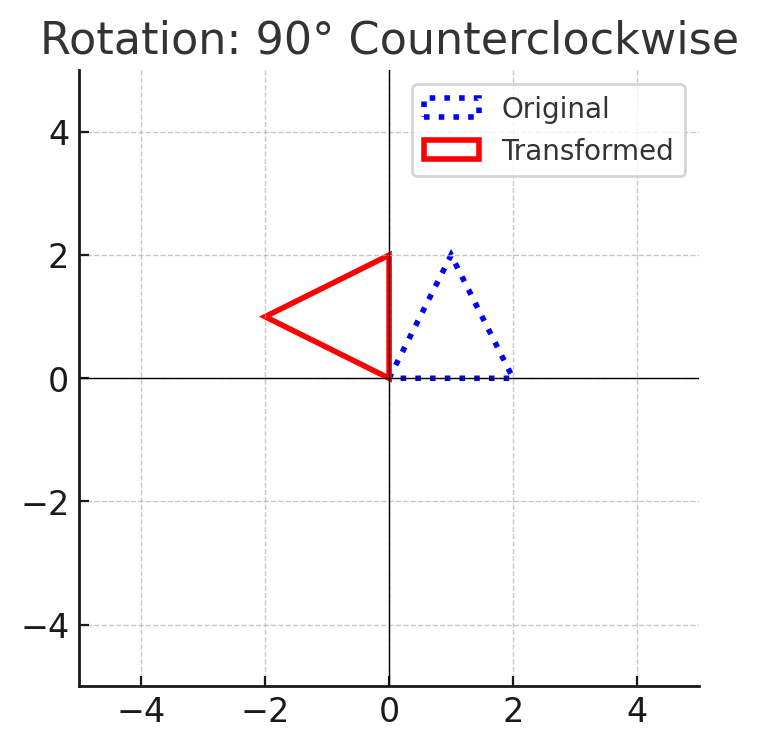
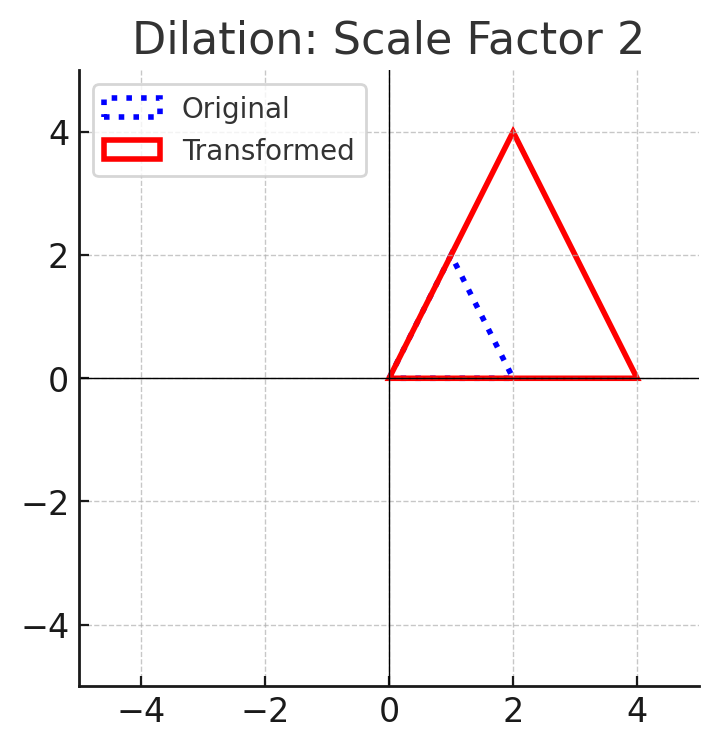
4. Dilations (Resizing)
- Enlarges or reduces a shape proportionally from a center point.
- The shape remains similar but not necessarily congruent.
- Example: Scaling a triangle by a factor of 2.
Congruence vs. Similarity
- Congruent figures: Same size and shape. Created by translations, reflections, or rotations.
- Similar figures: Same shape, but different size. Created by dilations (sometimes with other transformations).
The Pythagorean Theorem
The Pythagorean theorem states that, in a right triangle, the sum of the squares of the two shorter sides (legs) equals the square of the longest side (hypotenuse):
$a^2 + b^2 = c^2$
Where:
- $a$ and $b$ are the legs (shorter sides).
- $c$ is the hypotenuse (longest side, opposite the right angle).
Applying the Pythagorean Theorem
1. Finding the third side of a right triangle
If you know two sides of a right triangle, use the formula to find the missing side.
Example: Find the hypotenuse when $a = 6$ and $b = 8$.
$6^2 + 8^2 = c^2$
$36 + 64 = c^2$
$100 = c^2$
$\sqrt{c^2} = \sqrt{100} = 10$
2. Finding distance on a coordinate grid
The distance formula comes from the Pythagorean theorem:
$d = \sqrt{(x_2 − x_1)^2 + (y_2 − y_1)^2}$
Where:
- $(x_1, y_1)$ and $(x_2, y_2)$ are two points on the grid.
- The difference in $x$-values and $y$-values form a right triangle.
- The distance between points is the hypotenuse.
Example: Find the distance between $(1, 2)$ and $(5, 5)$.
$d = \sqrt{(5 − 1)^2 + (5 − 2)^2}$
$d = \sqrt{4^2 + 3^2}$
$d = \sqrt{16 + 9} = \sqrt{25} = 5$
3-D objects
Three-dimensional objects, as the name indicates, have a third dimension that can be measured and calculated.This means that finding area and perimeter, as you would with two-dimensional calculations, no longer covers the full object. Surface area measures all of the space on the outside of the object, while volume measures the capacity inside the object. The formulas to find volume and surface area vary by shape:
| Shape | Volume Formula | Variables |
| Cube | \(V = s^3\) | \(s\) = side length |
| Rectangular Prism | \(V = l \times w \times h\) | \(l\) = length, \(w\) = width, \(h\) = height |
| Cylinder | \(V = \pi r^2h\) | \(r\) = radius, \(h\) = height |
| Sphere | \(V = \left(\dfrac{4}{3}\right) \pi r^3\) | \(r\) = radius |
| Cone | \(V = \left(\dfrac{1}{3}\right) \pi r^2h\) | \(r\) = radius, \(h\) = height |
| Pyramid | \(V = \left(\dfrac{1}{3}\right)Bh\) | \(B\) = base area, \(h\) = height |
| Shape | Surface Area Formula | Variables |
| Cube | \(SA = 6s^2\) | \(s\) = side length |
| Rectangular Prism | \(SA = 2(lw + lh + wh)\) | \(l\) = length, \(w\) = width, \(h\) = height |
| Cylinder | \(SA = 2 \pi r^2 + 2 \pi rh\) | \(r\) = radius, \(h\) = height |
| Sphere | \(SA = 4 \pi r^2\) | \(r\) = radius |
| Cone | \(SA = \pi r^2 + \pi rl\) | \(r\) = radius, \(l\) = slant height |
| Pyramid | \(SA = B + (1/2)Pl\) | \(B\) = base area, \(P\) = base perimeter, \(l\) = slant height |
