HiSET Math Practice Test
Try our free HiSET Math practice test. The HiSET Math test has 50 multiple-choice questions that must be answered within 90 minutes. Topics covered include numerical operations, geometry, data analysis, probability, statistics, and algebra. You may use a calculator and you may use this formula sheet. Start your test prep now with our 25-question HiSET Math practice test!
Quiz Summary
0 of 25 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 25 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
-
Question 1 of 25
1. Question
Which of the following is equivalent to \(3x(2 + 5y)\)?
CorrectIncorrect -
Question 2 of 25
2. Question
If a car travels 360 kilometers in 5 hours, how many kilometers will it travel in 9 hours when driving at the same speed?
CorrectIncorrect -
Question 3 of 25
3. Question
Aisha wants to paint the walls of a room. She knows that each can of paint contains one gallon. A half gallon will completely cover a 55 square feet of wall. Each of the four walls of the room is 10 feet high. Two of the walls are 10 feet wide and two of the walls are 15 feet wide. How many 1-gallon buckets of paint does Aisha need to buy in order to fully paint the room?
CorrectIncorrect -
Question 4 of 25
4. Question
There are 4 red marbles and 8 green marbles in a box. If Emma randomly selects a marble from the box, what is the probability of her selecting a red marble?
CorrectIncorrect -
Question 5 of 25
5. Question
If Maria left a $10.16 tip on a breakfast that cost $86.89, approximately what percentage was the tip?
CorrectIncorrect -
Question 6 of 25
6. Question
Sofía’s Restaurant offers the following choices:
Salad Entrée Dessert Spanich Lasagna Shortcake Caesar BBQ Ribs Pudding Iceberg Chicken Pie Mixed Salmon Spaghetti If the only dinner you can order must include one salad, one main course, and one dessert, how many different combinations of this dinner are possible?
CorrectIncorrect -
Question 7 of 25
7. Question
Factor: 4y(3x + 2) − 2(3x + 2)
CorrectIncorrect -
Question 8 of 25
8. Question
Simplify:
\(\dfrac{6x^5 − 2x − 4}{2x}\)
CorrectIncorrect -
Question 9 of 25
9. Question
Mason earns $8.10 per hour and worked 40 hours. Noah earns $10.80 per hour. How many hours would Noah need to work to equal Mason’s earnings over 40 hours?
CorrectIncorrect -
Question 10 of 25
10. Question
The area of the circle shown below is 100\(\pi\). What is the diameter (D) of the circle?
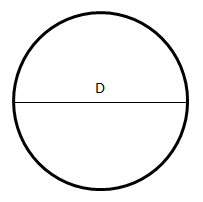 CorrectIncorrect
CorrectIncorrect -
Question 11 of 25
11. Question
Emma has a budget of $300 for her holiday spending. She decides to buy a pair of shoes for each of her grandchildren. If each pair costs c dollars, and Emma has 7 grandchildren, which of the following inequalities represents her budget constraint?
CorrectIncorrect -
Question 12 of 25
12. Question
There are 5 blue marbles, 4 red marbles, and 3 yellow marbles in a box. If Isabella randomly selects a marble from the box, what is the probability of her selecting a red or yellow marble?
CorrectIncorrect -
Question 13 of 25
13. Question
There are two pizza ovens in a restaurant. Oven #1 burns three times as many pizzas as Oven #2. If the restaurant had a total of 12 burnt pizzas on Saturday, how many pizzas did Oven #2 burn?
CorrectIncorrect -
Question 14 of 25
14. Question
Simplify:
\((x^6)(x^5)\)
CorrectIncorrect -
Question 15 of 25
15. Question
Each player on a high school football team has been weighed, and the data are shown in the box-and-whisker plot below.
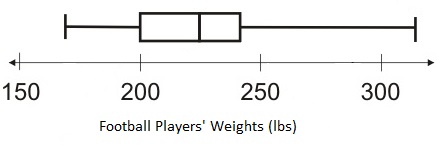
Based on this box-and-whisker plot, which of the following statements is accurate?
CorrectIncorrect -
Question 16 of 25
16. Question
If y = 3ab + 2b3, what is y when a = 1 and b = 2?
CorrectIncorrect -
Question 17 of 25
17. Question
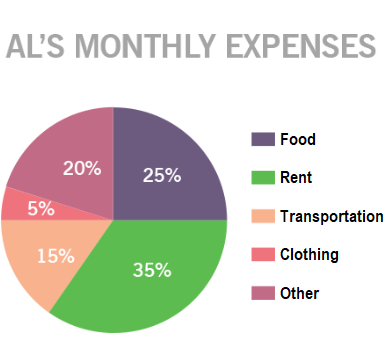
This pie chart shows Al’s monthly expenses. If Al spent a total of $1,550 in one month, how much did he spend on clothes in that month?
CorrectIncorrect -
Question 18 of 25
18. Question

This pie chart shows Al’s monthly expenses. If Al spent $210 on transportation in one month, how much did he spend on food in that month?
CorrectIncorrect -
Question 19 of 25
19. Question
A toy manufacturer makes 15,000 toys per year. The company randomly selects 300 of the toys to sample for inspection. The company discovers that there are 5 faulty toys in the sample. Based on the sample, how many of the 15,000 total toys are likely to be faulty?
CorrectIncorrect -
Question 20 of 25
20. Question
What is the slope of the line that passes through points (0,5) and (7,0) on the coordinate plane shown below?
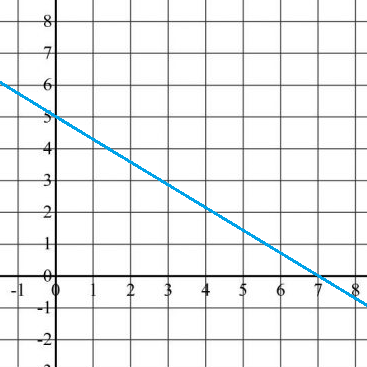 CorrectIncorrect
CorrectIncorrect -
Question 21 of 25
21. Question
Kayla owns a house cleaning company and must give price quotes to potential customers. She determines her price by assuming a $25 base charge and then adding $8 for each bathroom and $4 for every other room.
If she uses P to represent the price, B to represent the bathrooms, and R to represent the other rooms, which of the following defines her price quote formula?CorrectIncorrect -
Question 22 of 25
22. Question
Max struggled with his math class early in the year, but he has been working hard to improve his scores. There is one test left, and he is hoping that his final average test score will be 75. What score will he need to get on Test 6 to finish the year with an average score of 75?
Test Score Test 1 50 Test 2 52 Test 3 77 Test 4 88 Test 5 91 Test 6 CorrectIncorrect -
Question 23 of 25
23. Question
\((3x + 4y)(2x + 5y) = \ ?\)
CorrectIncorrect -
Question 24 of 25
24. Question
What is 181.5% of 18?
CorrectIncorrect -
Question 25 of 25
25. Question
Which of the following tables does NOT represent a function?
CorrectIncorrect
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Current
- Correct
- Incorrect
Next Practice Test: Reading
