HiSET Math Study Guide: Data Analysis, Probability, Statistics

Questions in this section will assess your ability to:

• Interpret and represent data using graphs, tables, and summaries
• Calculate probabilities of compound events using various methods
• Develop probability models to estimate event likelihoods
• Use measures of center to analyze and compare data sets
• Generalize population information from sample data using statistics

Practice Quiz

What is Probability?

Probability is a measure of how likely an event is to happen. It is expressed as a number between 0 (impossible) and 1 (certain). The higher the probability, the more likely the event will occur.

Approximating Probability

To estimate the probability of an event, use this formula:

$\text{Probability} = \dfrac{\text{Number of times the event occurs}}{\text{Total number of trials}}$

For example, if you flip a coin 100 times and it lands on heads 55 times, the approximate probability of flipping heads is:

$\dfrac{55}{100} = 0.55 \text{ (or 55%)}$

Developing a Probability Model

probability model is a way to organize probabilities for different outcomes of a chance event.

1. List all possible outcomes.
   Example: Rolling a six-sided die has six outcomes: {1, 2, 3, 4, 5, 6}.
2. Assign probabilities to each outcome.

   If the die is fair, each number has an equal probability:

   $P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = \dfrac{1}{6}$

3. Check that all probabilities add up to 1.

   $\dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = 1$

Finding the Probability of an Event

An event is a specific outcome or a group of outcomes.

• Example 1: What is the probability of rolling an even number (2, 4, or 6)?
  • There are 3 favorable outcomes out of 6 total.
  • $P(\text{even number}) = \dfrac{3}{6} = \dfrac{1}{2} = 0.5 \text{ (or 50%)}$
• Example 2: If you draw a card from a standard deck of 52 cards, what is the probability of drawing a heart?
  • There are 13 hearts in the deck.
  • $P(\text{heart}) = \dfrac{13}{52} = \dfrac{1}{4} = 0.25 \text{ (or 25%)}$

Key Tip
When estimating probability from an experiment, the more trials you perform, the more accurate your estimate will be!

Probability of Compound Events

What is a Compound Event?

compound event is when more than one event happens at the same time. There are two types:

1. Independent Events – One event does not affect the other. (e.g., flipping a coin and rolling a die)
2. Dependent Events – One event affects the probability of the other. (e.g., drawing two cards from a deck without replacement)

Finding Probability Using Different Methods

1. Tables (Two-Way Tables)

A two-way table helps organize data when two different events occur. It allows us to find probabilities by counting favorable outcomes.

Example:

A school surveyed students on whether they like Math or Science.

	Like Math	Don’t Like Math	Total
Like Science	20	10	30
Don’t Like Science	15	5	20
Total	35	15	50

Find the probability that a student picked at random likes both Math and Science:

• Favorable outcomes = 20
• Total students = 50
• Probability = 20/50 = 0.4 (or 40%)

2. Lists (Systematic Listing of Outcomes)

A list helps when there are only a few possible outcomes.

Example: Rolling a die and flipping a coin.

Possible outcomes:

1. (1, H)
2. (1, T)
3. (2, H)
4. (2, T)
5. (3, H)
6. (3, T)
7. (4, H)
8. (4, T)
9. (5, H)
10. (5, T)
11. (6, H)
12. (6, T)

If we want to find the probability of rolling a 4 and flipping heads:

• Favorable outcome: (4, H)
• Total outcomes: 12
• Probability: 1/12 ≈ 8.3%

3. Tree Diagrams

A tree diagram shows all possible outcomes in a visual way.

Example: Tossing Two Coins

Each branch represents an outcome:

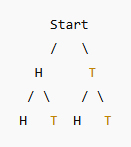
Possible outcomes: HH, HT, TH, TT

Probability of getting two heads (HH):

• Favorable outcomes = 1
• Total outcomes = 4
• Probability = 1/4 = 25%

What is the Mean?

The mean, or average, is a way to find the central value of a set of numbers. It helps summarize a data set and allows us to compare different groups.

How to Calculate the Mean:

1. Add up all the numbers in the data set.
2. Divide by the total number of values in the set.

Example:

Find the mean of these numbers:
4, 7, 10, 5, 9

Step 1: Add them up:
$4 + 7 + 10 + 5 + 9 = 35$

Step 2: Divide by the number of values (5):
$35 ÷ 5 = 7$

So, the mean is 7.

Using the Mean to Compare Data Sets

The mean helps us compare different groups of numbers. A higher mean suggests that, on average, the values in one data set are greater than those in another.

Example:

Class A test scores: 80, 85, 90, 75, 95
Class B test scores: 70, 75, 80, 85, 90

Find the mean of each class:

• Class A Mean:$(80 + 85 + 90 + 75 + 95) ÷ 5 = 85$
• Class B Mean:$(70 + 75 + 80 + 85 + 90) ÷ 5 = 80$

Since Class A’s mean (85) is higher than Class B’s mean (80), we can infer that Class A performed better on average.

Determining a Missing Value Given the Mean

Sometimes, you may know the mean and need to find a missing number in the data set.

Example:

A teacher knows that the mean of 4 test scores is 85. The first three scores are 90, 80, and 85. What is the missing fourth score?

Step 1: Set up the equation:

$\dfrac{90 + 80 + 85 + x}{4} = 85$

Step 2: Solve for $x$:

$\dfrac{255 + x}{4} = 85$

Multiply both sides by 4:

$255 + x = 340$

Subtract $255$ from both sides:

$x = 85$

So, the missing score is $85$.

Key Tip
The mean is sensitive to outliers (extremely high or low values). If one number is much higher or lower than the others, it can pull the mean up or down, sometimes making it misleading. In such cases, consider using the median (middle value) for a better picture of the data.

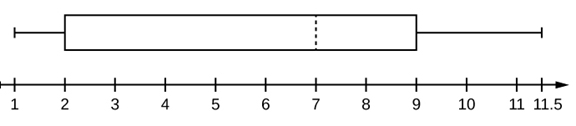
Box Plots (Box-and-Whisker Plots)

A box plot, also called a box-and-whisker plot, is a simple way to display the distribution of a dataset. It highlights five key numbers: the minimum, first quartile (Q1), median (Q2), third quartile (Q3), and maximum.

Here is a labeled box and whisker plot, showing the key parts:

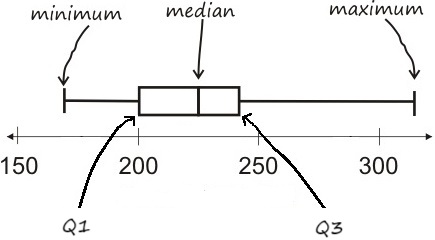
• Minimum (Whisker): The lowest data point within the range.
• Q1 (First Quartile): The 25th percentile, marking the lower bound of the interquartile range.
• Median: The middle value of the dataset.
• Q3 (Third Quartile): The 75th percentile, marking the upper bound of the interquartile range.
• Maximum (Whisker): The highest data point within the range.

Data Analysis, Probability, Statistics Review Quiz