HiSET Math Study Guide: Measurement & Geometry

Measurement and geometry questions will assess your ability to:

• Describe and perform transformations in the plane
• Determine triangle similarity and congruence to solve problems
• Use properties of two-dimensional figures and angle relationships
• Solve for the volume and surface area of 3D figures
• Apply the Pythagorean theorem in various contexts

Practice Quiz

Transformations in the Plane

A transformation moves or changes a shape while maintaining its size or proportions. There are four main types:

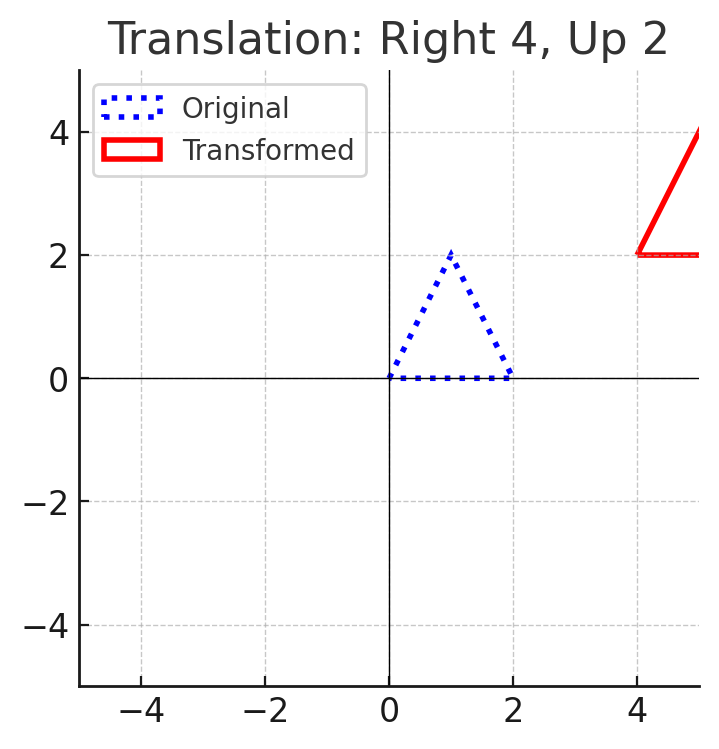
1. Translations (Slides)

• Moves a shape without rotating or flipping it.
• Every point shifts the same distance and direction.
• Example: Moving a triangle 4 units right and 2 units up.

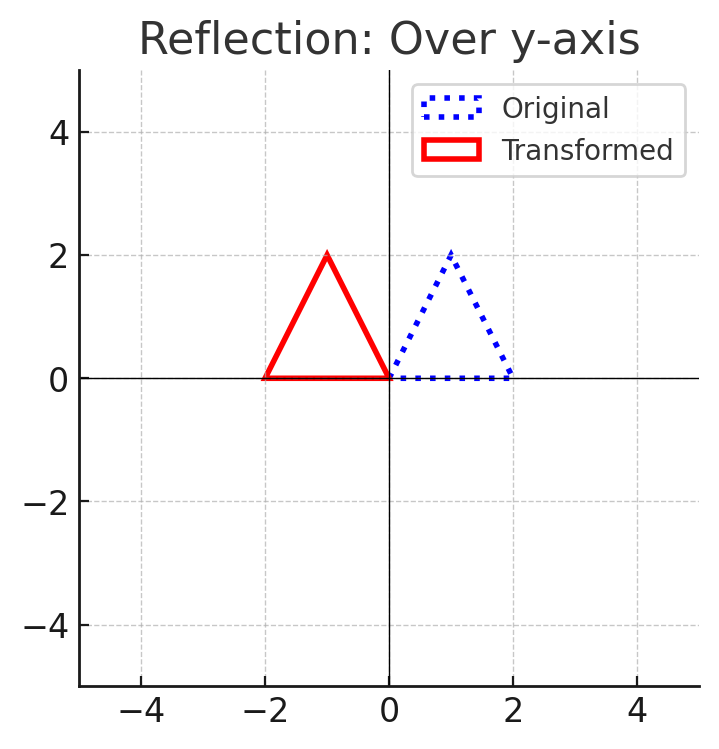
2. Reflections (Flips)

• Flips a shape over a line of reflection ($x$-axis, $y$-axis, or another line).
• The shape remains congruent but reversed.
• Example: Reflecting a triangle over the $y$-axis.

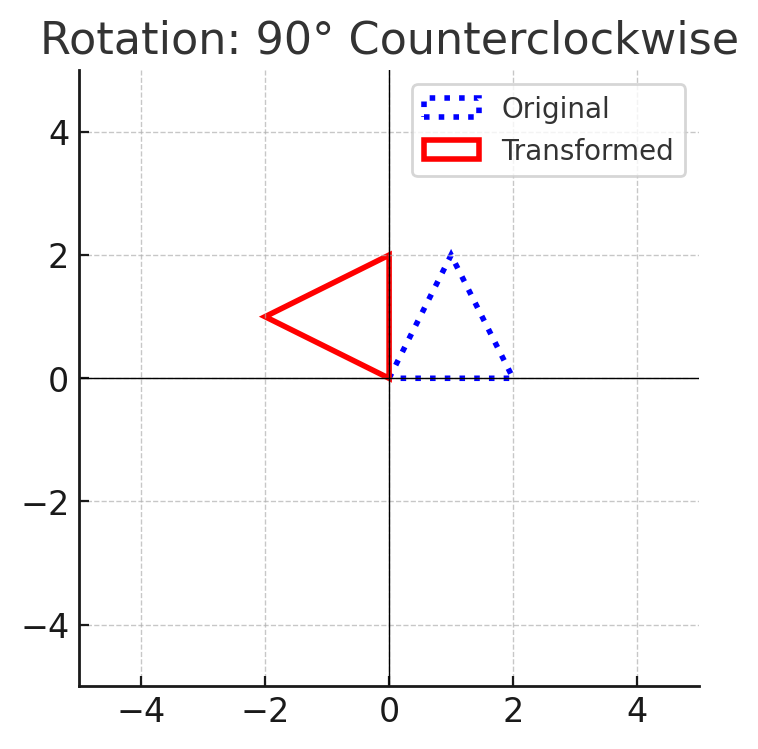
3. Rotations (Turns)

• Spins a shape around a fixed point, usually the origin $(0)$.
• Measured in degrees $(90°, 180°, 270°)$.
• Example: Rotating a triangle $90°$ counterclockwise around the origin.

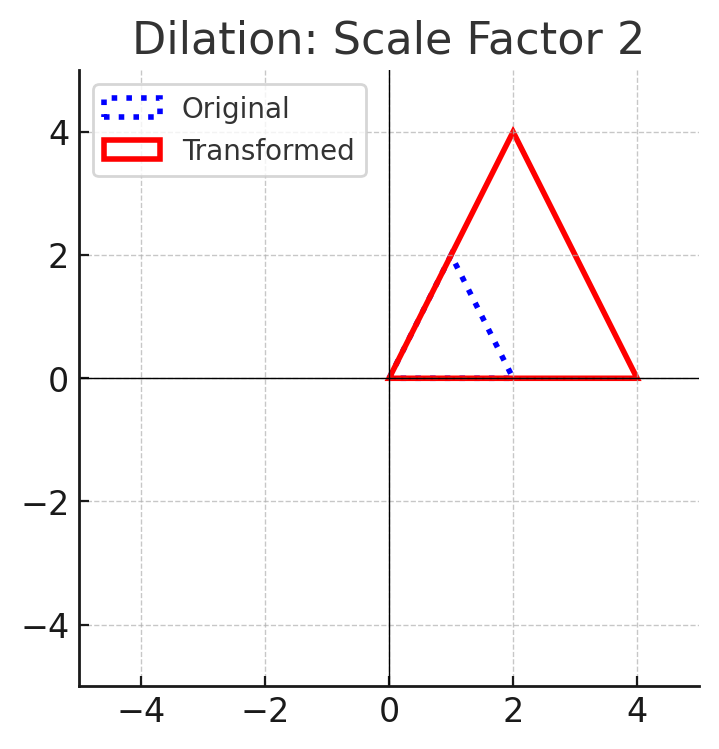
4. Dilations (Resizing)

• Enlarges or reduces a shape proportionally from a center point.
• The shape remains similar but not necessarily congruent.
• Example: Scaling a triangle by a factor of 2.

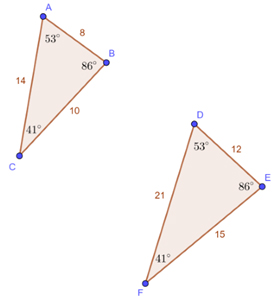
Congruence vs. Similarity

• Congruent Figures: Same size and shape. Created by translations, reflections, or rotations.
• Similar Figures: Same shape, but different size. Created by dilations (sometimes with other transformations).

The Pythagorean Theorem

The Pythagorean theorem states that, in a right triangle, the sum of the squares of the two shorter sides (legs) equals the square of the longest side (hypotenuse):

$a^2 + b^2 = c^2$

Where:

• $a$ and $b$ are the legs (shorter sides)
• $c$ is the hypotenuse (longest side, opposite the right angle).

Applying the Pythagorean Theorem

1. Finding the third side of a right triangle

If you know two sides of a right triangle, use the formula to find the missing side.

Example: Find the hypotenuse when $a = 6$ and $b = 8$.

$6^2 + 8^2 = c^2$

$36 + 64 = c^2$

$100 = c^2$

$\sqrt{c} = \sqrt{100} = 10$

2. Finding distance on a coordinate grid

The distance formula comes from the Pythagorean theorem:

$d = \sqrt{(x_2 − x_1)^2 + (y_2 − y_1)^2}$

Where:

• $(x_1, y_1)$ and $(x_2, y_2)$ are two points on the grid.
• The difference in x-values and y-values form a right triangle.
• The distance between points is the hypotenuse.

Example: Find the distance between $(1, 2)$ and $(5, 5)$.

$d = \sqrt{(5 – 1)^2 + (5 – 2)^2}$

$d = \sqrt{4^2 + 3^2}$

$d = \sqrt{16 + 9} = \sqrt{25} = 5$

Measurement & Geometry Review Quiz